how are binary option values calculated
Abstract
Nosotros extend the binary options into barrier binary options and discuss the application of the optimal structure without a smooth-fit status in the option pricing. We offset review the existing work for the knock-in options and nowadays the principal results from the literature. Then we evidence that the toll function of a knock-in American binary choice can be expressed in terms of the toll functions of unproblematic barrier options and American options. For the knock-out binary options, the smooth-fit belongings does not hold when we utilize the local time-space formula on curves. By the properties of Brownian motility and convergence theorems, nosotros bear witness how to calculate the expectation of the local time. In the fiscal analysis, we briefly compare the values of the American and European barrier binary options.
Share and Cite:
Gao, M. and Wei, Z. (2020) The Barrier Binary Options. Journal of Mathematical Finance, x, 140-156. doi: x.4236/jmf.2020.101010.
1. Introduction
Barrier options on stocks have been traded in the OTC (Over-The-Counter) marketplace for more than four decades. The cheap cost of bulwark options compared with other exotic options has contributed to their all-encompassing use by investors in managing risks related to commodities, FX (Strange Exchange) and interest rate exposures.
Barrier options accept the ordinary phone call or put pay-offs but the pay-offs are contingent on a second event. Standard calls and puts accept pay-offs that depend on one market level: the strike price. Bulwark options depend on ii market levels: the strike and the barrier. Bulwark options come up in ii types: in options and out options. An in selection or knock-in choice only pays off when the option is in the coin with the barrier crossed before the maturity. When the stock price crosses the bulwark, the barrier option knocks in and becomes a regular choice. If the stock price never passes the barrier, the option is worthless no matter it is in the money or not. An out barrier pick or knock-out option pays off just if the option is in the money and the barrier is never being crossed in the fourth dimension horizon. Every bit long as the barrier is not being reached, the selection remains a vanilla version. Nonetheless, in one case the barrier is touched, the pick becomes worthless immediately. More details virtually the barrier options are introduced in [1] and [ii].
The use of barrier options, binary options, and other path-dependent options has increased dramatically in recent years specially by big financial institutions for the purpose of hedging, investment and adventure direction. The pricing of European knock-in options in closed-form formulae has been addressed in a range of literature (see [iii] [iv] [5] and reference therein). There are two types of the knock-in choice: up-and-in and down-and-in. Any upward-and-in call with strike above the bulwark is equal to a standard call option since all stock movements leading to pay-offs are knock-in naturally. Similarly, any down-and-in put with strike below the bulwark is worth the same as a standard put option. An investor would buy knock-in option if he believes the movements of the asset price are rather volatile. Rubinstein and Reiner [6] provided closed form formulas for a wide variety of single barrier options. Kunitomo and Ikeda [7] derived explicit probability formula for European double bulwark options with curved boundaries every bit the sum of infinite serial. Geman and Yor [8] applied a probabilistic arroyo to derive the Laplace transform of the double barrier option price. Haug [ix] has presented analytic valuation formulas for American upwardly-and-input and down-and-in phone call options in terms of standard American options. It was extended past Dai and Kwok [10] to more types of American knock-in options in terms of integral representations. Jun and Ku [eleven] derived a closed-form valuation formula for a digit bulwark option with exponential random time and provided analytic valuation formulas of American partial barrier options in [12]. Hui [13] used the Blackness-Scholes environment and derived the analytical solution for knock-out binary option values. Gao, Huang and Subrahmanyam [14] proposed an early exercise premium presentation for the American knock-out calls and puts in terms of the optimal free boundary.
There are many dissimilar types of bulwark binary options. It depends on: 1) in or out; two) up or down; iii) call or put; 4) greenbacks-or-nothing or asset-or-null. The European valuation was published by Rubinstein and Reiner [half-dozen]. However, the American version is non the combination of these options. This paper considers a wide variety of American barrier binary options and is organised as follows. In Department 2 we innovate and fix the notation of the bulwark binary problem. In Department 3 nosotros formulate the knock-in binary options and briefly review the existing work on knock-in options. In Section 4 we formulate the knock-out binary choice trouble and give the value in the course of the early exercise premium representation with a local fourth dimension term. We conduct a fiscal assay in Section 5 and talk over the application of the barrier binary options in the electric current financial market.
2. Preliminaries
American feature entitles the option buyer the right to do early. Regardless of the pay-off structure (greenbacks-or-null and asset-or-nothing), for a binary telephone call option in that location are 4 basic types combined with bulwark feature: up-in, upwards-out, down-in and downwardly-out. Consider an American (also known as "Ane-touch") up-in binary call. The value is worth the same every bit a standard binary telephone call if the barrier is below the strike since information technology naturally knocks-in to get the pay-off. On the other hand, if the bulwark is above the strike, the valuation turns into the same form of the standard with the strike price replaced by the barrier since we cannot exercise if we merely pass the strike and we will immediately stop if the option is knocked-in. Now let us consider an up-out call. Evidently, it is worthless for an upwardly-out telephone call if the barrier is beneath the strike. Meanwhile, if the barrier is college than the strike the stock will not hit information technology since it stops once it reaches the strike. For these reasons, information technology is more mathematically interesting to discuss the down-in or downwards-out call and up-in or up-output.
Earlier introducing the American barrier binary options, we give a brief introduction of European barrier binary options and some settings for this new kind of selection.
Figure 1 and Figure two show the value of eight kinds of European barrier binary options and the comparisons with respective binary pick values. All of the European bulwark binary option valuations are detailed in [6]. Note that the payment is binary, therefore it is not an ideal hedging musical instrument so we do not analyse the Greeks in this paper and more applications of such options in fiscal market will exist addressed in Department 5. Since we will study the American-style options, we but consider the cases that barrier beneath the strike for the call and barrier to a higher place the strike for the put every bit reasons stated above. As we can encounter in Figure 1 and Effigy ii, the bulwark-version options in the bluish or ruddy curves are e'er worth less than the corresponding vanilla option prices. For the binary phone call selection in Figure i when the asset price is below the in-bulwark, the knock-in value is same equally the standard cost and the knock-out value is worthless. When the stock price goes very loftier, the upshot of the barrier is intangible. The knock-intends to worth zero and the knock-out value converges to the knock-less value. On the other mitt in Console (a) of Effigy ii, the value of the binary put decreases with an increasing stock price. Equally Panel (b) in Figure 2 shows, the asset-or-naught put option value first increases and then decreases as stock price going large. At a lower stock price, the effect of the barrier for the knock-out value is trifle and the knock-in value tends to exist nothing. When the stock price is above the barrier, the knock-out is worthless and the up-in value gets the peak at the barrier. The figures also point the relationship
(ii.1)
Above all, barrier options create opportunities for investors with lower premiums than standard options with the aforementioned strike.
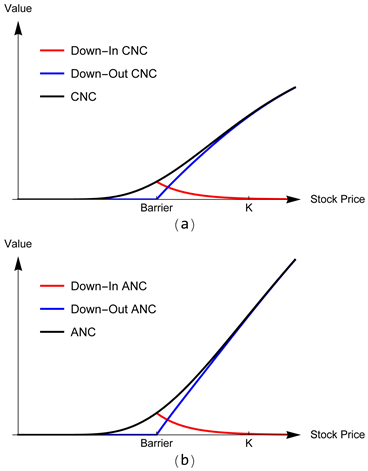
Effigy 1. A computer comparing of the values of the European barrier cash-or-cipher call(CNC) and asset-or-nothing call(ANC) options for t given and fixed.
Figure 2. A computer comparing of the values of the European bulwark cash-or-nothing put (CNP) and asset-or-cypher put (ANP) options for t given and fixed.
three. The American Knock-In Binary Option
We kickoff from the greenbacks-or-nil pick. At that place are four types for the cash-or-nil choice: up-and-in call, down-and-in call, up-and-input and down-and-input. For the up-and-in phone call, if the barrier is below the strike the selection is worth the same as the American greenbacks-or-nix call since it will cantankerous the barrier simultaneously to become the pay-off. On the other paw, if the barrier is higher up the strike the value of the selection turns into the American cash-or-nothing call with the strike replaced past the barrier level. Mathematically, the almost interesting office of the cash-or-nothing telephone call selection is down-and-in telephone call (also known as a down-and-up pick). For the reason stated above, we just discuss upwards-and-input and downward-and-in phone call in this section.
Nosotros presume that the up-in trigger clause entitles the option holder to receive a digital put option when the stock price crosses the bulwark level.
one) Consider the stock toll X evolving as
(3.1)
with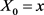 
under P for any interest rate 
and volatility
. Throughout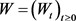 
denotes the standard Brownian motion on a probability space
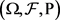. The arbitrage-free cost of the American greenbacks-or-nada knock-in put option at time 
is given by
(iii.2)
where K is the strike price, 50 is the barrier level and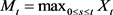 
is the maximum of the stock price procedure 10. Remember that the unique strong solution for (iii.ane) is given by
(3.3)
under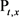
. The procedure X is strong Markov with the infinitesimal generator given past
(3.iv)
We introduce a new process 
which represents the process Ten stopped once it hits the barrier level 50. Ascertain
, where 
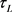is the first striking time of the barrier L as
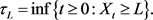(three.v)
It means that we exercise not need to monitor the maximum process 
since the process 
behaves exactly the same as the process X for whatsoever time 
and nigh of the properties of Ten follow naturally for
.
two) Standard Markovian arguments lead to the following free-boundary problem
(three.6)
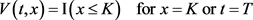(3.7)
(3.8)
(three.nine)
(3.x)
where the continuation set is expressed every bit
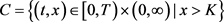(3.xi)
and the stopping set is given by
(3.12)
and the optimal stopping fourth dimension is given past
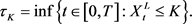(three.13)
The proof is easy to attend past applying the definition of optimal stopping fourth dimension.
3) Summarising the preceding facts, nosotros can at present apply the approach used in [10] and [15] to obtain a representation for the cost of the American knock-in binary option as follows:
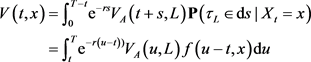(three.14)
for 
and
, where 
is the probability density role of the outset hitting fourth dimension of the process (3.1) to the level 50. The density function is given past (see due east.g. [sixteen])
(three.fifteen)
for 
and
, where 
is the standard normal density function given by 
for
. Therefore, the expression for the
arbitrage-free price is given past (3.xiv) and can be solved by inserting the price of the American greenbacks-or-nothing put option.
The value of the American greenbacks-or-nix put pick is given past [six]
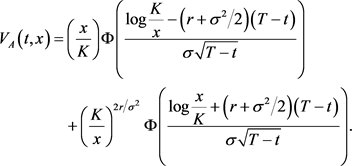(3.16)
The other 3 types of binary options: cash-or-nothing telephone call, asset-or-nothing telephone call and put follow the same pricing procedure and their American values can exist referred in [6].
4. The American Knock-Out Binary Options
4.1. The American Knock-Out Cash-Or-Goose egg Options
1) Consider the stock price X evolving as
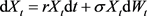(4.1)
with 
under P for any interest charge per unit 
and volatility
. Throughout 
denotes the standard Brownian motion on a probability space
. The arbitrage-costless price of the American up-out cash-or-aught put option at time 
is given by
(four.2)
where K is the strike price, L is the barrier level and 
is the maximum of the stock cost process 10. Call back that the unique strong solution for (4.one) is given past
(4.3)
under
. The procedure X is strong Markov with the infinitesimal generator given past
(4.4)
We introduce a new process 
which represents the process X stopped once it hits the barrier level 50. Define
, where 
is the showtime hitting fourth dimension of the barrier L:
(iv.v)
It ways that nosotros practice not need to monitor the maximum process 
since the procedure 
behaves exactly the same as the process 10 for whatever time 
and most of the backdrop of X follow naturally for
.
2) Let us determine the structure of the optimal stopping problem (4.2). Standard Markovian arguments pb to the post-obit free-boundary problem (see [17])
(4.six)
(four.7)
(four.8)
(4.9)
(4.x)
where the continuation set is expressed as
(four.11)
the stopping set up is given by
(4.12)
and the optimal stopping time is given past
(4.13)
denoting the starting time time the stock price is equal to 1000 before the stock price is equal to 50. We will evidence that K is the optimal boundary and 
is optimal for (4.2) below.
3) Nosotros will evidence that (4.13) is optimal for (iv.two). The fact that the value part (4.ii) is a discounted price indicates that the larger 
is, the less value we will get. Equally to the payoff, it is either £i or nada. Therefore, the optimal stopping fourth dimension is just the very starting time time that the stock price hits K, which is (iv.thirteen). To evidence this, nosotros define 
every bit any stopping time. We demand to show that
(iv.fourteen)
Actually,
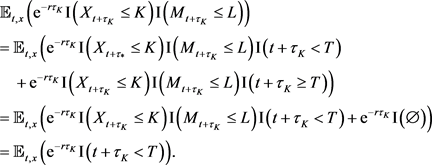(4.xv)
On the other hand,
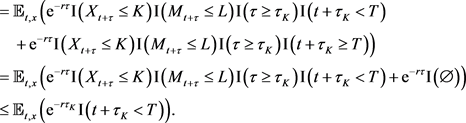(4.sixteen)
Hence we conclude that 
is optimal in (4.ii).
4) Based on the optimal stopping time (4.13), a direct solution for (iv.2) tin be expressed as
(4.17)
For the geometric Brownian movement the density 
is known in airtight grade (cf. ( [xvi], Folio 622):
(4.18)
for
, where 
is given past (cf. [16])
(4.xix)
for
. The consequence is straightforward
(4.20)
for
. The value role concerns with the convergence due to the sum of an space series. More precisely we will employ the optimal stopping theory to value (4.2) and get a amend upshot. However, the result from (4.20) indicates some properties of the pricing (4.2). It is easy to verify that local time-space formula is applicative to our trouble (4.2).
5) To get the solution to the optimal stopping problem (4.2), apply Ito's formula to 
and get
(iv.21)
where the office 
is defined past
(4.22)
is given by
(4.23)
and 
refers to integration with respect to the continuous increasing function
, and 
is a continuous local martingale for 
with
.
The martingale term vanishes when taking Eastward on both sides. From the optional sampling theorem we get
(iv.24)
for all stopping times 
of X with values in 
with 
and 
given and fixed. Replacing s by 
in (4.24), we become
(four.25)
for all
, where 
and 
for
. We obtain the following early practice premium representation of the value function
(4.26)
The showtime term on the RHS is the arbitrage-gratis cost of the European knock-out cash-or-nothing put choice 
at the point 
and can be written explicitly as (see [6])
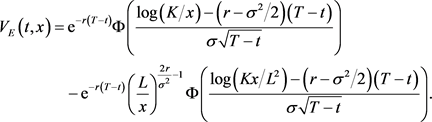(4.27)
We write
(4.28)
Recall that the joint density function of geometric Brownian motion and its maximum 
under P with 
is given past (see [16])
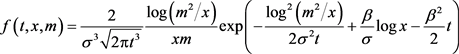(4.29)
for 
with
.
half dozen) We will discuss the calculation well-nigh the local-fourth dimension term 
(run across [xviii] and reference therein). Note that
(4.30)
From the definition of local time 
, there exists a sequence 
such that 
and 
-
. Using Dominated Convergence Theorem, we get
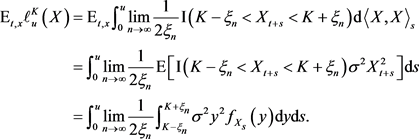(4.31)
The second step is attained past Fubini'south Theorem and Dominated Convergence Theorem. Past the definition of derivative, the last step in (4.31) equals
(4.32)
The density function 
is given by
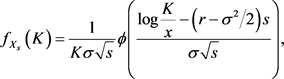(four.33)
where 
is the density function for standard normal distribution. Therefore, (four.xxx) can be expressed every bit
(4.34)
Substituting the event (four.34) into (4.26), nosotros get the early exercise premium (EEP) representation for the American knock-out greenbacks-or-null put option
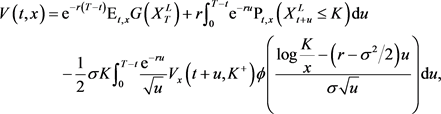(4.35)
where the first and second terms are defined in (four.27) and (4.28).
The main upshot of the present subsection may now be stated every bit follows. Below, nosotros will make use of the following function
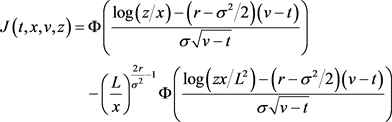(4.36)
for all 
and
.
Theorem i. The arbitrage-free price of the American knock-out cash-or-nothing put choice follows the early-exercise premium representation
(4.37)
for all
, where the first term is the arbitrage-gratuitous price of the European knock-out cash-or-nix put option and the second and tertiary terms are the early on-practice premium.
The proof is straightforward following the points 4, 5 and 6 stated to a higher place. Notation that our problem is based on the stopped process 
instead of the original process X and that the value of 
in (iv.37) needs to be estimated by finite difference method otherwise nosotros tin can non get the value
.
The cash-or-nothing call option tin be handled in a similar way. The different function is the European value function in (4.27). The arbitrage-free cost of the European downward-out cash-or-zippo call pick 
at the betoken 
is given by (see [half dozen])
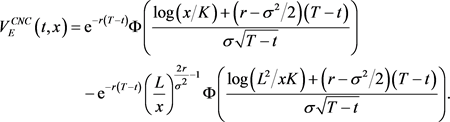(4.38)
iv.2. The American Knock-Out Asset-Or-Goose egg Options
The arbitrage-free price of the European knock-out asset-or-nothing option 
at the point 
tin can be written explicitly as (see [half-dozen])
(4.39)
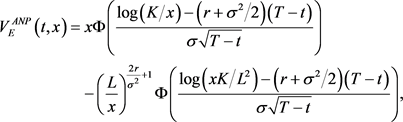(four.xl)
where 
represents the value for the European down-out nugget-or-nothing call (ANC) option and 
for the upward-out put.
Theorem 2. The arbitrage-costless cost of the American knock-out asset-or-nothing option follows the early-practise premium representation
(4.41)
for all
, and
(4.42)
for all
, where the first term is the arbitrage-gratuitous cost of the European knock-out nugget-or-nothing option and the second term is the early on-practise premium.
Proof. The proof is analogous to that of Theorem 1. Back to (iv.22), it is piece of cake to verify that the value of H vanishes since 
in the stopping fix. There are only 2 terms in (iv.26).
5. Financial Analysis of the American Barrier Binary Options
The payment of the American barrier binary options is binary, so they are not platonic hedging instruments. Instead, they are ideal investment products. It is pop to apply structured accrual range notes in the financial markets. Such notes are related to foreign exchanges, equities or commodities. For example, in a daily accrual USD-BRP substitution rate range notation, it pays a fixed daily accrual involvement if the exchange rate remains within a certain range.
By and large, an investor ownership a barrier option is seeking for more risk than that of a vanilla selection since the bulwark options tin can be stopped or "knocked-out" at whatsoever fourth dimension prior to maturity or never start or "knock-in" due to not hitting the barrier. Bones reasons to buy bulwark options rather than standard options include a better expectation of the hereafter behaviour of the market, hedging needs and lower premiums. In the liquid market, traders value options past calculating the expected value of the pay-offs based on all stock scenarios. It ways to some extent we pay for the volatility around the forward price. However, barrier options eliminate paying for the impossible scenarios from our point of view. On the other mitt, we can improve our return by selling a bulwark option that pays off based on scenarios we recall of fiddling probability. Let us imagine that the 1-twelvemonth forward price of the stock is 110 and the spot toll is 100. We believe that the market is very likely to rise and if information technology drops below 95, information technology will decline further. We can buy a down-and-out call option with strike price 110 and the barrier level 95. At any time, if the stock falls below 95, the option is knocked-out. In this manner, we do not pay for the scenario that the stock cost drops firstly and so goes up once more. This reduces the premium. For the hedgers, barrier options meet their needs more than closely. Suppose we own a stock with spot 100 and decide to sell it at 105. We also want to get protected if the stock price falls beneath 95. We can purchase a put option struck at 95 to hedge it simply information technology is more than inexpensive to buy an up-an-out put with a strike toll 95 and barrier 105. Once the stock price rises to 105 when we tin can sell it and this put disappears simultaneously.
The relationship betwixt knock-in selection, knock-out choice and knock-less option (standard option) of the same blazon (telephone call or put) with the same expiration date, strike and barrier level can be expressed as
(five.1)
This relationship only holds for the European barrier options. Information technology has not been obtained for the American version when we get the American values from the sections in a higher place.
We plot the value of the American barrier binary options using the free-boundary structure in the to a higher place sections. Note that the value of 
in Equations (four.37), (4.41) and (4.42) separately is estimated by finite difference method (run into [19]).
The American value curves in Figure three and Figure 4 are false from (xv) by inserting dissimilar American binary choice values. Figure three shows that the value of the American downwards-in cash-or-nix call options (asset-or-nothing call option follows a similar curve) increases with stock price 
earlier the in bulwark and then decreases due to the dubiety of knock-in. Figure four shows the value of the American up-in cash-or-nothing put option (nugget-or-nothing put is similar ). As nosotros can see before the barrier, the option value is increasing and gets its peak at the bulwark. Then the value goes down as the stock price continues to go up after the bulwark level. Generally, the price of the American version options is larger than the European version.
Figures 5-8 show the values for the knock-out binary options. Effigy five illustrates that the value of the up-out cash-or-nothing put choice is a decreasing function of the stock price below the barrier. However, in Figure 6 the up-out asset-or-nothing put first goes upward and then down to the barrier. Nosotros tin can see the value of the down-out cash-or-nothing call option in Effigy 7 is strictly increasing as the asset price above the bulwark. The asset-or-naught call value in Figure 8 is likewise in the similar state of affairs but with different corporeality of payoff size. All of the out figures show that the smooth-fit condition is non satisfied at the stopping boundary K.
Effigy 3. A computer comparison for the values of the European and the American downward-in cash-or-nix call options with parameters 
and
.
Effigy 4. A computer comparison for the values of the European and the American upwards-in cash-or-nothing put options with parameters 
and
.
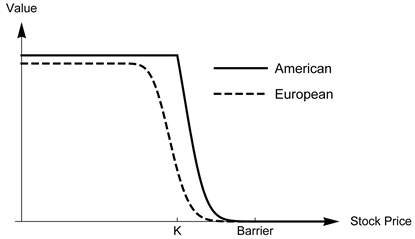
Figure 5. A computer comparison for the values of the European and the American upward-out greenbacks-or-nothing put options with parameters 
and
.
Effigy 6. A reckoner comparing for the values of the European and the American upwards-out nugget-or-nothing put options with parameters 
and
.
Effigy vii. A calculator comparison for the values of the European and the American down-out cash-or-goose egg call options with parameters 
and
.
The results of this paper also hold for an underlying asset with dividend structure. With modest modifications, the formulas adult here can be applied to handle those problems.
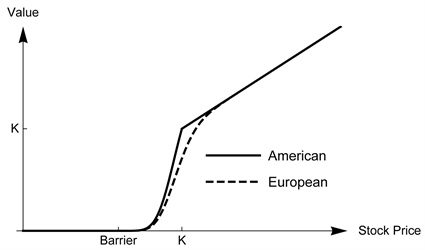
Effigy 8. A calculator comparison for the values of the European and the American down-out asset-or-nothing call options with parameters 
and
.
Acknowledgements
The authors are grateful to Goran Peskir, Yerkin Kitapbayev and Shi Qiu for the informative discussions.
Conflicts of Interest
The authors declare no conflicts of interest.
References
| [1] | Derman, Due east. and Kani, I. (1996) The Ins and Outs of Bulwark Options: Part 1. Derivatives Quarterly, iii, 55-67. |
| [ii] | Derman, E. and Kani, I. (1997) The Ins and Outs of Bulwark Options: Part ii. Derivatives Quarterly, 3, 73-80. |
| [3] | Haug, E.Grand. (2007) The Complete Guide to Option Pricing Formulas. McGraw-Hill Companies, New York. |
| [iv] | Merton, R.C. (1973) Theory of Rational Choice Pricing. The Bell Journal of Economics and Direction Science, four, 141-183. https://doi.org/10.2307/3003143 |
| [five] | Rich, D.R. (1994) The Mathematical Foundations of Barrier Option-Pricing Theory. Advances in Futures and Options Research: A Research Annual, 7, 267-311. |
| [6] | Rubinstein, M. and Reiner, East. (1991) Unscrambling the Binary Code. Gamble Magazine, iv, 20. |
| [7] | Kunitomo, North. and Ikeda, Grand. (1992) Pricing Options with Curved Boundaries. Mathematical Finance, 2, 275-298. https://doi.org/10.1111/j.1467-9965.1992.tb00033.x |
| [8] | Geman, H. and Yor, M. (1996) Pricing and Hedging Double-Bulwark Options: A Probabilistic Approach. Mathematical Finance, vi, 365-378. https://doi.org/10.1111/j.1467-9965.1996.tb00122.ten |
| [9] | Haug, E.Grand. (2001) Airtight Form Valuation of American Barrier Options. International Journal of Theoretical and Applied Finance, 4, 355-359. https://doi.org/10.1142/S0219024901001012 |
| [x] | Dai, M. and Kwok, Y.1000. (2004) Knock-in American Options. Journal of Futures Markets, 24, 179-192. https://doi.org/10.1002/fut.10101 |
| [11] | Jun, D. and Ku, H. (2012) Digital Bulwark Pick Contract with Exponential Random Time. IMA Periodical of Applied Mathematics, 78, 1147-1155. https://doi.org/ten.1093/imamat/hxs013 |
| [12] | Jun, D. and Ku, H. (2013) Valuation of American Fractional Barrier Options. Review of Derivatives Research, sixteen, 167-191. https://doi.org/ten.1007/s11147-012-9081-1 |
| [xiii] | Hui, C.H. (1996) Ane-Touch on Double Barrier Binary Pick Values. Applied Fiscal Economics, 6, 343-346. https://doi.org/10.1080/096031096334141 |
| [xiv] | Gao, B., Huang, J.Z. and Subrahmanyam, Chiliad. (2000) The Valuation of American Barrier Options Using the Decomposition Technique. Journal of Economic Dynamics and Command, 24, 1783-1827. https://doi.org/10.1016/S0165-1889(99)00093-seven |
| [15] | Aitsahlia, F., Imhof, L. and Lai, T.L. (2004) Pricing and Hedging of American Knock-in Options. The Periodical of Derivatives, xi, 44-50. https://doi.org/10.3905/jod.2004.391034 |
| [16] | Borodin, A.N. and Salminen, P. (2002) Handbook of Brownian Motion: Facts and Formulae. Springer, Berlin. https://doi.org/ten.1007/978-3-0348-8163-0 |
| [17] | Peskir, G. and Shiryaev, A. (2006) Optimal Stopping and Free-Purlieus Bug. Birkhäuser, Basel. |
| [18] | Peskir, G. (2005) A Change-of-Variable Formula with Local Fourth dimension on Curves. Journal of Theoretical Probability, eighteen, 499-535. https://doi.org/10.1007/s10959-005-3517-6 |
| [xix] | Qiu, S. (2016) Early Exercise Options with Two Free Boundaries. PhD Thesis, The University of Manchester, Manchester. |
Source: https://www.scirp.org/journal/paperinformation.aspx?paperid=98476
Posted by: ellismajeough.blogspot.com
0 Response to "how are binary option values calculated"
Post a Comment